
그래픽 & 멀티미디어
컴퓨터 그래픽에서 선을 그리는 방법에는 여러 가지가 있습니다. 직선의 공식을 그대로 이용하는 방법도 있고, 실수 곱셈을 덧셈으로 바꾼 DDA 방법도 있습니다만, 빠르게 그리는 방법 중에 하나가 브레슨햄(Bresenhan) 알고리듬을 이용하는 것입니다. 브레슨햄 알고리듬에서는 정수 계산만 사용하기 대문에 처리가 매우 빠르죠.
동영상에는 선을 그리는 몇 가지 방법과 브레슨햄을 이용한 방법을 소개해 드리고 있습니다. 그러나 실제 실무에 사용하는 선 그리기는 브레슨햄 알고리듬을 이용한 방법이므로 이부분만 따로 정리해 보았습니다.
브레슨햄(Bresenham)알고리듬
직선의 공식을 사용하여 머릿 속으로 그래프를 그려 보면, 무수히 많은 점을 생각할 수 있읍니다만, 컴퓨터 그래픽에서는 스크린 좌표가 모두 정수이므로, 복잡하고 계산을 느리게 만드는 실수 계산을 정수 계산 만으로도 구현할 수 없을까하는 생각에서 만들어진 것이 브레슨햄 알고리듬입니다.
직선의 공식을 이용하여 계산된 좌료값이 소주점 이하 몇개의 자리로 된 실수값을 어렵게 구했다고 하더라도 컴퓨터화면에 출력할 때에는 소수점이하를 모두 버림한단든지 반올림해서 정수로 만들게 됩니다. 이렇게 버려지는 소수점 이하의 복잡한 계산을 브레슨햄 공식을 이용하여 없애 보도록 하겠습니다.
*** 이하의 설명은 dx 가 dy 보다 큰 경우일 때 입니다. ***
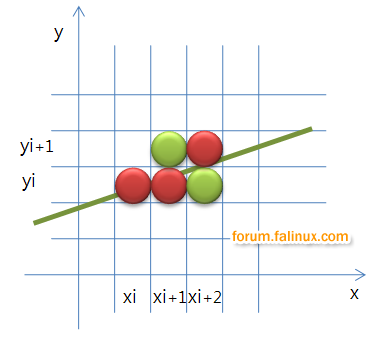
<그림-1>
직선을 컴퓨터 화면에 긋는 다고 하고, 이미 (xi, yi) 좌표에 점을 찍었습니다. 브레슨햄의 기본 원리는 선의 공식에 따라 다음 좌표값을 구하는 것이 아니라 현재 점의 위치에 대해서 어느 좌표에 다음 점을 찍을 지를 판단하는 알고리듬입니다.
<그림-1>에서 (xi,yi)의 다음 점의 위치는 녹색점(xi+1, yi+1) 보다는 빨강색점(xi+1, yi) 가 실제 점에 가깝습니다. 그렇다면 여기서 녹색점과 빨강색점에 대해 실제 직선의 위치와의 차이 d1, d2를 구해 보겠습니다.
d1, d2를 구하는 이유는, d1 < d2 라면 실제 y 점이 yi 에 가깝다는 얘기가 되고, yi 에 점을 찍으면 됩니다. 반대로 d1 > d2 라면 yi+1에 점을 찍으면 되기 때문입니다.
즉, 0 < d1-d2 이면 yi+1 에, 0 > d1-d2 이면 yi 에 점을 찍으면되므로 (1) d1 과 d2의 차, 특히 (2) 차이값이 양수인지, 음수인지를 구하면 되겠습니다.
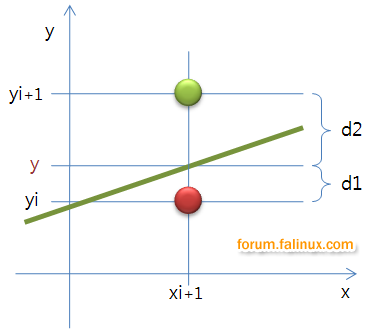
d1 = y -yi
여기서 y=m(xi+1) +b 이므로,
d1 = m(xi+1) +b -yi
d2 는,
d2 = (yi+1) -y
= yi +1 -( m(xi+1)+b)
= yi -m(xi +1) -b +1
두 거리의 차이를 구해 보겠습니다.
d1 - d2 = m(xi+1) +b -yi -(yi -m(xi +1) -b +1)
= m(xi+1) +b -yi -yi +m(xi+1) +b -1
= 2 m(xi+1) -2yi +2b -1
m 은 기울기를 dy/dx 이므로,
d1 - d2 = 2(dy/dx)(xi+1) -2yi +2b -1
여기서 다음 점을 찾기 위해서는 두 거리의 차이가 궁굼한 것이 아니라 두 차이에 대한 부호, 즉 양수인지 음수인지만이 필요하므로 정수 나눗셈이 있는 부분을 양편에 dx를 곱해서 없애겠습니다.
dx(d1-d2) = 2dy(xi+1) -2dxyi +2dxb -dx
= 2dyxi +2dy -2dxyi +2dxb -dx
다시 이 공식에서 변수 부분인 xi 또는 yi 가 들어간 부분과 한번 계산되면 다시 계사할 필요가 없는 부분으로 정리해 보겠습니다. 그리고 부호값 만을 생각할 수 있는 변수 pi 로 정리해 보겠습니다.
dx(d1 - d2) = pi = 2dyxi +2dy -2dxyi +2dxb -dx
= 2dyxi -2dxyi +2dy +2dxb -dx
= 2dyxi -2dxyi +2dy +dx(2b -1)
상수부분인 2dy +dx(2b-1)를 C 로 대치하면,
pi = 2dyxi -2dxyi +C <--- 공식 1
가 됩니다.
우리가 이 알고리듬을 이용해서 선을 긋게 되면, 루프를 이용하게 될 것이고, 이전에 계산된 pi 값을 이번 계산에 대입하고 적용할 수 있습니다. 그러므로 다음 pi 값인 pi+1 값을 아래와 같이 구할 수 있습니다.
pi+1 = 2dyxi+1 -2dxyi+1 +C <--- 공식 2
이전 p 값을 계속 참조하여 계산 하므로 pi 와 pi+1 값의 차를 구하겠습니다.
pi+1 - pi= 2dyxi+1 -2dxyi+1 +C - 2dyxi +2dxyi -C
= 2dy(xi+1-xi) - 2dx(yi+1-yi) <--- 공식 3
여기서 xi+1 와 xi는 서로 이웃하는 점이므로 xi+1 - xi는 1입니다.
그러므로 아래와 같이 정리할 수 있습니다.
pi+1 - pi= 2dy - 2dx(yi+1-yi)
이제 pi+1 값만 구한다면,
pi+1 = pi + 2dy - 2dx(yi+1-yi)
아직까지 복잡하게 보이지만 역시 스크린 좌표는 정수이고 yi+1와 yi 의 차이가 0 또는 1이라는 점을 상기한다면,
- 계산된 pi 값이 양수라면 d1이 더 크므로 다음 점은 현재의 yi 보다 1 만큼 크게되므로,
pi+1 = pi + 2dy - 2dx
가 되며, - pi 값이 음수라면 d1이 더 작으므로 yi 값과 같아지므로 yi+1 - yi 는 0이 되므로,
pi+1 = pi + 2dy
값이 됩니다.
여기서 계산된 pi+1은 다음 루프의 pi 값이 되므로 이를 루프에서 계속 계산되고 다음 계산에 대입된다면 처음 p0 값을 구하고 점을 찍고 다음 pi 값으로 대입하면서 점 위치를 찾아 점을 찍으면 됩니다.
p0값을 구하기 위해 공식 1 에 처음 좌표 (x1, y1)을 대입하고, 다음 예상 좌표를 (x1+1, y1+1/2)로 생각하고 p0을 구합니다..
p(x1, y1) = 2dyx1 -2dxy1 +C
p(x1+1, y1+1/2)= 2dy(xi+1) -2dx(yi+1/2) +C
p0 = p(x1+1, y1+1/2) - p(x1, y1)
= 2dy(xi+1) -2dx(yi+1/2) +C - ( 2dyx1 -2dxy1 +C)
= 2dyx1 +2dy -2dxy1 -dx -2dyx1 +2dxy1 +C -C
= 2dy(x1-x1) +2dy -2dx(y1-y1) -dx
= 2dy -dx
p0 을 구하기 위해 x1 의 다음 좌표는 당연히 1 을 증가한 x1+1 이 되겠지만 , y1 축의 값은 y1 이 될지 y1+1이 될지 모르므로 확륭 상의 경우를 1/2로 보고 계산한 것입니다.
선을 긋기 전에 필요한 상수 값
- 최초의 p0 을 구합니다.
- pi 의 부호 값에 따라 아래의 2가지 값이 필요합니다.
- 2(dy -dx)
- 2dy
이후 선을 긋는 루프에서
- 계산된 p 값이 양수이면,
- y 좌표값을 1 증가하고,
- p 값에 2(dy-dx) 값을 더합니다.
- 음수 이면,
- p 값에 2dy 만 더합니다.
#include <stdio.h>
#include <stdlib.h>
#include <string.h> // abs
#include <unistd.h> // open/close
#include <fcntl.h> // O_RDWR
#include <sys/ioctl.h> // ioctl
#include <sys/mman.h> // mmap PROT_
#include <linux/fb.h>
int screen_width;
int screen_height;
unsigned short *fb_mapped;
void dot( int x, int y)
{
unsigned short *ptr;
ptr = fb_mapped + screen_width * y + x;
*ptr = 0xffff;
}
void line( int x1, int y1, int x2, int y2)
{
int dx, dy;
int p_value;
int inc_2dy;
int inc_2dydx;
int inc_value;
int ndx;
dx = abs( x2 -x1);
dy = abs( y2 -y1);
if ( dy <= dx)
{
inc_2dy = 2 * dy;
inc_2dydx = 2 * ( dy - dx);
if ( x2 < x1)
{
ndx = x1;
x1 = x2;
x2 = ndx;
ndx = y1;
y1 = y2;
y2 = ndx;
}
if ( y1 < y2) inc_value = 1;
else inc_value = -1;
dot( x1, y1);
p_value = 2 * dy - dx;
for (ndx = x1; ndx < x2; ndx++)
{
if ( 0 > p_value) p_value += inc_2dy;
else
{
p_value += inc_2dydx;
y1 += inc_value;
}
dot( ndx, y1);
}
}
else
{
inc_2dy = 2 * dx;
inc_2dydx = 2 * ( dx - dy);
if ( y2 < y1)
{
ndx = y1;
y1 = y2;
y2 = ndx;
ndx = x1;
x1 = x2;
x2 = ndx;
}
if ( x1 < x2) inc_value = 1;
else inc_value = -1;
dot( x1, y1);
p_value = 2 * dx - dy;
for (ndx = y1; ndx < y2; ndx++)
{
if ( 0 > p_value) p_value += inc_2dy;
else
{
p_value += inc_2dydx;
x1 += inc_value;
}
dot( x1, ndx);
}
}
}
int main( int argc, char **argv)
{
int fb_fd;
struct fb_var_screeninfo fbvar;
struct fb_fix_screeninfo fbfix;
int bytes_per_line;
int mem_size;
if ( access( "/dev/fb", F_OK))
{
printf( "프레임 버퍼 장치가 없습니다.n");
return 0;
}
if ( 0 > ( fb_fd = open( "/dev/fb", O_RDWR)))
{
printf( "프레임 버퍼에 접근할 수 없습니다.n");
return 0;
}
if ( ioctl( fb_fd, FBIOGET_VSCREENINFO, &fbvar))
{
printf( "FBIOGET_VSCREENINFO를 실행하지 못했습니다.n");
return 0;
}
if ( ioctl( fb_fd, FBIOGET_FSCREENINFO, &fbfix))
{
printf( "FBIOGET_FSCREENINFO 실행하지 못했습니다.n");
return 0;
}
screen_width = fbvar.xres; // 스크린의 픽셀 폭
screen_height = fbvar.yres; // 스크린의 픽셀 높이
bytes_per_line = fbfix.line_length; // 한개 라인 당 바이트 개수
mem_size = bytes_per_line * screen_height;
fb_mapped = ( unsigned short *)mmap( 0,
mem_size,
PROT_READ|PROT_WRITE,
MAP_SHARED,
fb_fd,
0);
if ( 5 != argc)
{
printf( "사용방법: $]./sample x1 y1 x2 y2 n");
}
else
{
line( atoi( argv[1]), atoi( argv[2]), atoi( argv[3]), atoi(argv[4]));
}
munmap( fb_mapped, mem_size);
close( fb_fd);
return 0;
}


