박두현의 컴퓨터 이론들 - 영역처리 : 2차 미분(Second Order Derivative)

안녕하세요. 박두현 입니다.

오늘은 엣지를 검출해내는 알고리즘의 수학적인 계산법, 2차 미분에 대해서 알아보도록 하겠습니다.

1. Second order derivative

2차 미분은 말 그대로 1차 미분값을 다시 한번 미분하는 방법을 말 합니다.

2차 미분 연산의 장점은 먼저 엣지의 중심에 위치한 임의의 엣지만을 찾을 수 있다는 것(Edge localization)입니다. 또한 밝기값이 점차적으로 변화되는 영역에 대해서는 반응을 보이지 않는다는 것 입니다.

2차 미분 연산자의 결과 영상은 엣지 부분에서 부호가 바뀌게 됩니다. 이것을 영교차(Zero crossing)이라고 부릅니다.

영교차가 발생된 부분에서 출력 화소값을 설정 합니다.

2. Laplacian Operator

오늘은 2차 미분 연산의 대표격인 라플라시안 연산에 대해서 알아보도록 하겠습니다.

저도 싫지만 그래도 이론을 설명하기 위해서 수학 공식을 좀 펼쳐보도록 하겠습니다. [그림2-1]에서 볼수 있는 것이 바로 라플라시안 연산의 정의와 그 계산 공식 입니다.

[그림2-1. Laplacian Operator]

3. LoG (Laplacian of Gaussian)

라플라시안 연산의 경우 잡음에 민감합니다. 그래서 실제 적용하는데는 문제가 발생하게 되지요.

그래서 잡음에 덜 민감한 2차 미분 검출기가 필요한데요, 그래서 적용하는 기법이 바로 이 LoG 입니다.

라플라시안을 적용하기 전에 먼저 Gaussian Smothing 을 수행해서 잡음을 제거하게 됩니다.

이 방법은 결과의 모양으로 인해 멕시칸 모자 필터라 불리우기도 합니다.

시그마 값에 따라서 함수의 폭과 최대, 최소값이 변화하게 됩니다.

시그마 값이 커지면 최대값이 작아지고 엣지가 넓게 검출 됩니다. 반대로 시그마 값이 작아지면 최대값이 커지고 경사가 급격한 엣지와 정확한 엣지가 검출 됩니다.

인간의 시각과 유사한 특성을 가지고 있다고 하네요.

[그림3-1. Formula of LoG]

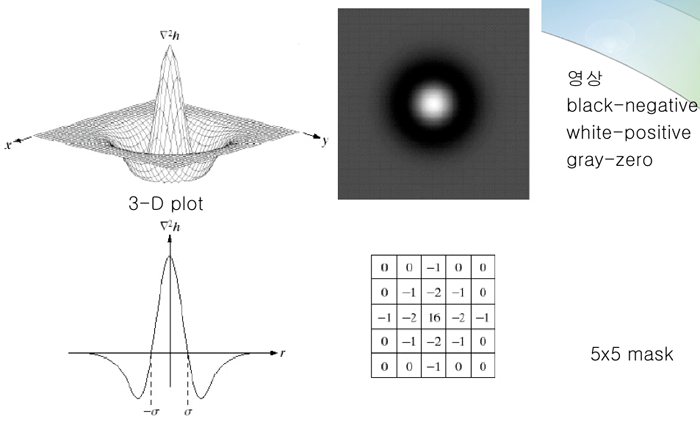
[그림3-2. Result of LoG]

4. 마치면서...

오늘은 여기까지 하도록 하겠습니다.

사실 이런 수학공식만 들여다 보기보다는 이 기능을 수행하는 프로그램을 직접 짜보면 정말 시각적으로 재미가 있습니다.

그러나 이 공간에서 그런 것들까지 함께 하기에는 여러가지 제약사항이 많이 있네요.

다음주에도 유익한 내용으로 찾아뵙도록 하겠습니다.