
강좌 & 팁
삼성의 1bit용 NAND Flash ECC 알고리즘을 해부해 볼 호서대학교에 재학 중인 MS-OSEK Team의 지정웅 입니다. 여기서 말하는 ECC는 Error Checking & Correction의 약자입니다. 에러를 검사하고 고치겠다는 패기를 엿볼 수 있습니다요. 1. 삼성 NAND ECC 알고리즘의 특징. NAND Flash(이하 NAND)의 특성은 페이지 단위로 읽고, 쓰고, 블록 단위로 지운다는 것입니다. 이때 페이지는 528 ~ 2112 Byte(data영역 + spare영역)의 크기를 지니고 있습니다. 때문에 1bit라도 Error가 난다면 상당한 문제가 아닐 수 없습니다. NAND는 가격대비 성능이 좋지만 데이터 연산 중 파워가 나가거나 여러 상황에 의해 데이터가 깨질 수 있습니다. 그렇기에 데이터에 대한 ECC 코드를 만들어 spare영역에 저장하여 NAND의 안정성을 높이는 것 입니다. 삼성의 NAND ECC 알고리즘에 몇 가지 특징이 있습니다. 1. ECC 코드는 패리티(parity)로 이루어져 있습니다. 2. 패리티가 쌍으로 존재 합니다. 3. NAND에 데이터를 쓸 때 ECC 코드를 만들고, 데이터를 읽을 때 ECC 코드를 만듭니다. 4. 쓸 때 데이터의 ECC 코드와 읽을 때 데이터의 ECC 코드를 XOR연산하여 최종 ECC 코드를 만듭니다. 이 결과에 따라 Error의 종류를 파악합니다. 5. 최종 ECC 코드는 패리티 쌍을 이용해 표현식(?)으로 바꾸어 에러 비트를 찾아냅니다. 이해를 돕기 위해 1byte의 ECC 코드를 만들어 보도록 하죠. 2. 1byte의 ECC 코드를 만들자.
이것을 NAND에 쓰기 전에 ECC 코드를 이루는 패리티를 아래의 방법대로 구합니다.
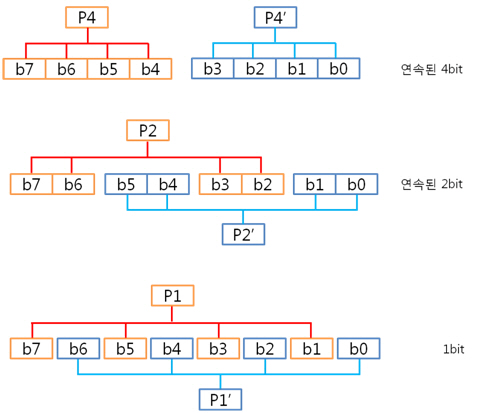
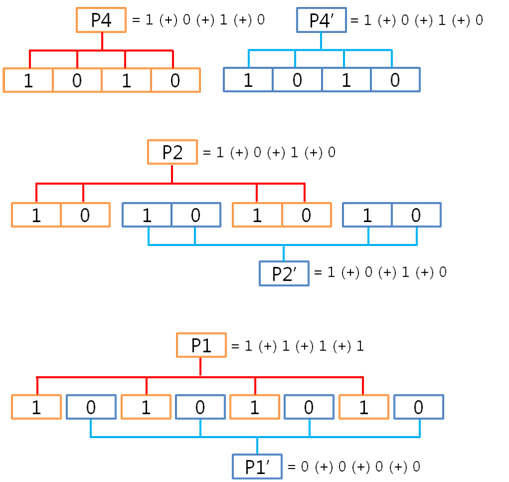
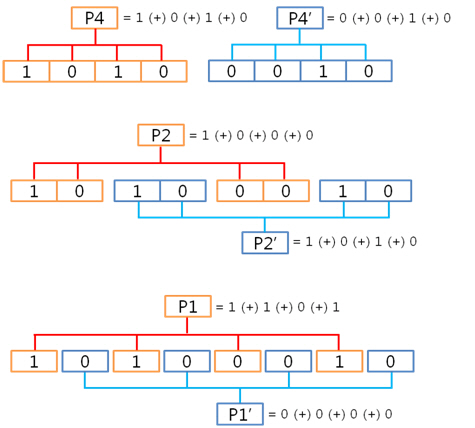
그런데 이게 무슨 의미일까요? P가 패리티를 의미하고 패리티가 쌍으로 존재한다고 했는데 그러면 P4와 P4’는 쌍이네. 엇 잠깐, 보니까 뭔가 규칙이 있는 것 같습니다? 규칙이 보이시나요? 오호라~ 아래와 같은 규칙이 숨어 있군요! 이제 보니 패리티 쌍인 P4, P4’는 1byte의 연속된 4bit를 XOR 연산한 결과, P2, P2’는 1byte의 연속된 2bit를 XOR 연산한 결과, P1, P1’는 1byte의 1bit를 XOR 연산한 결과로 구하는 것이였네요. 자 그렇다면 위의 계산 식대로 다음 데이터의 패리티 쌍을 구해볼까요.
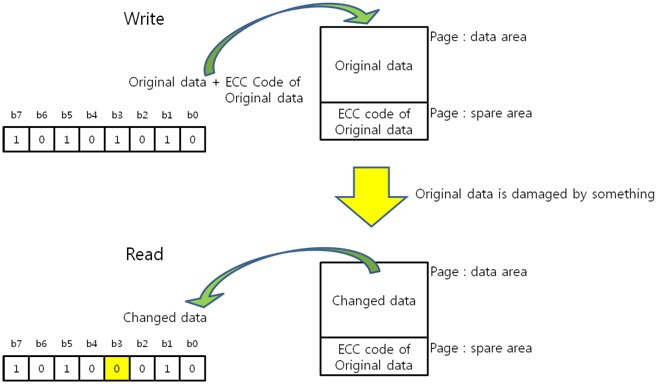
XOR 연산을 통해 원본 데이터의 ECC 코드를 구했습니다. 그런데 1byte의 1bit 에러를 검사하고 고치기 위해 6비트나 쓰다니 상당히 배꼽이 크군요. 라는 생각은 잠시! 의문이 곧 풀리니 쭉쭉 읽어 주시기 바랍니다. 자 그럼, ECC도 구했으니 원본 데이터를 NAND에 저장합니다. 그런데 어떤 요인에 의해 NAND에 저장한 데이터가 깨졌네요.
위에 보시는 바와 같이 3번째 비트가 0으로 변했습니다. 3번째 비트, 3번째 비트, 3번째 비트 기억! 하지만 우리는 이 데이터가 원본인지 아닌지 모르기 때문에 읽은 데이터의 ECC 코드를 생성합니다. 방법은 아까와 같습니다.
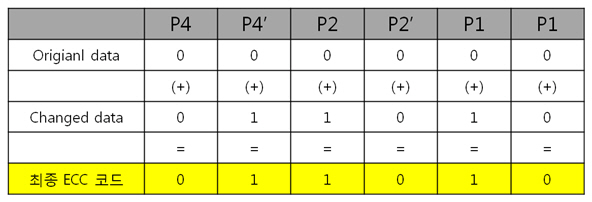
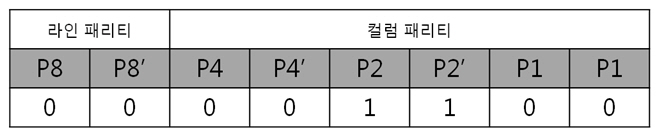
XOR 연산을 통해 읽은 데이터의 ECC 코드를 구했습니다. 어라 원본 데이터의 ECC 코드와 딱 봐도 틀리네요? 위에서 언급했듯이 최종 ECC 코드는 쓸 때 데이터의 ECC 코드와 읽을 때 데이터의 ECC 코드를 XOR 연산하여 구한다고 했습니다. 아래와 같이 P4는 P4와, P4’는 P4’와 연산을 하는 것이죠. 드디어 최종 ECC 코드를 구했습니다. 하지만 이것을 가지고 어떻게 에러가 난 비트를 찾아내는 것일까요? 위에서 언급한 삼성 NAND의 특징에서 최종 ECC 코드의 패리티 쌍을 표현식으로 바꾸어 에러가 난 비트를 찾아 낸다 하였습니다. 규칙은 아래와 같습니다. ex) 패리티의 쌍을 이용해 표현식으로 바꾼다. (P4와 P4’쌍, P2와 P2’쌍, P1과 P1’쌍) 예를 들어 P4 = 0, P4’ = 0 일 경우, 표현은 0 P4 = 1, P4’ = 0 일 경우, 표현은 1 P4 = 0, P4’ = 1 일 경우, 표현은 0 P4 = 1, P4’ = 1 일 경우, 표현은 1 그럼 우리가 만든 최종 ECC 코드의 패리티 쌍을 표현식으로 바꾸면
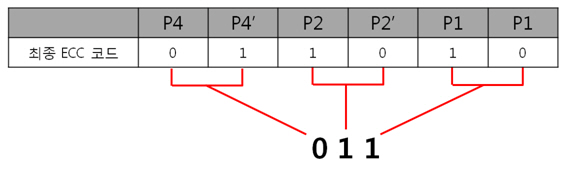
짜잔, ‘011’ 이라는 결과가 나왔습니다. 10진수로 바꾸어 보면 3이라는 숫자가 나오네요. 에러가 난 비트는 바로 3번쩨 비트에서 일어났다는 것을 알 수 있습니다. 우와~ 쒼기하다. 사실 P4, P4’, P2, P2’, P1, P1’ 이것들은 ‘컬럼 패리티’라고 불립니다. ‘열’이라는 뜻을 가진 컬럼의 의미대로 ‘컬럼 패리티’는 에러난 열의 위치를 찾는다는 것입니다. X,Y 그래프로 따지면, 컬럼 패리티로 X의 위치를 찾겠다는 것입니다. 3. 2byte의 ECC 코드를 만들자. 1byte 에서 1bit 에러는 위와 같이 찾았는데 그렇다면! 2byte 에서 1bit 에러는 어떻게 찾을까요?
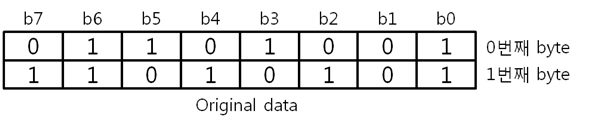
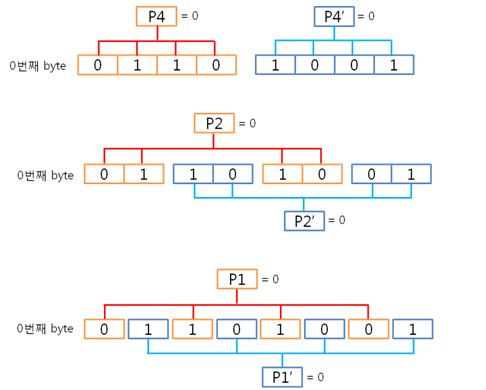
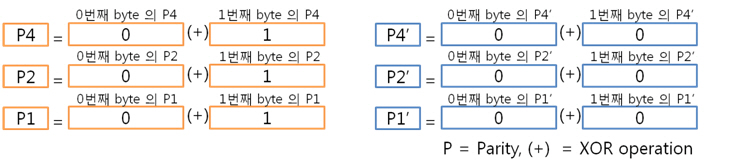
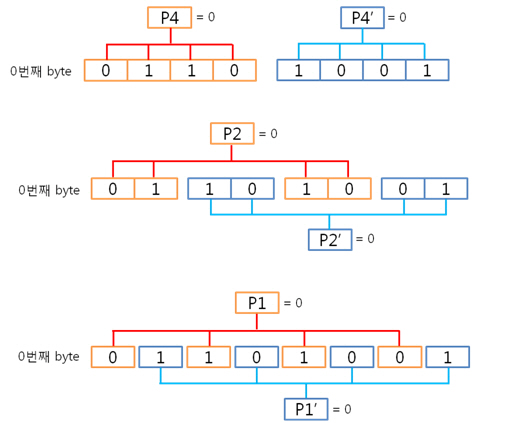
우선 컬럼 패리티를 구해야 찾을 수 있겠죠. 자 그렇다면 2byte의 컬럼 패리티는 어떻게 구해야 할까요? X의 위치를 나타내는 컬럼 패리티를 아래와 같은 방법으로 구합니다. 우와, 그냥 각 byte의 컬럼 패리티를 XOR 연산을 하면 되는군요. 먼저 0번째 byte의 컬럼 패리티를 구해 봅시다.
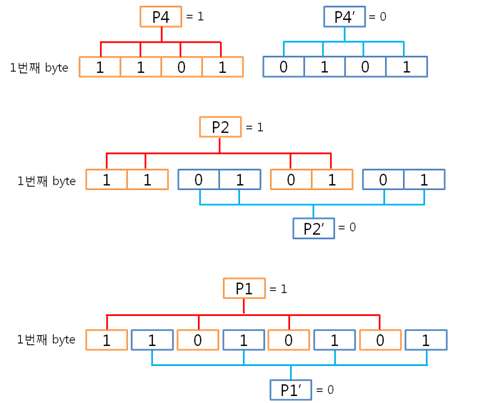
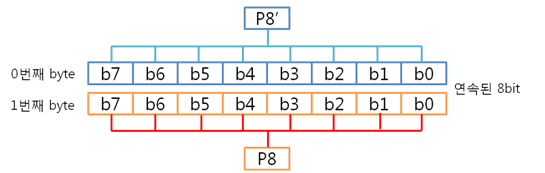
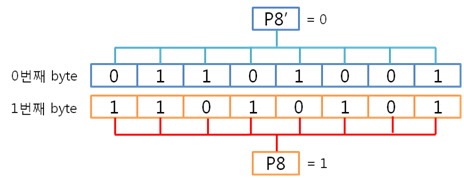
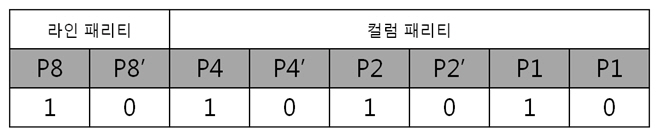
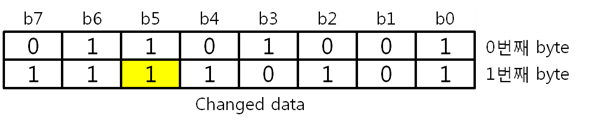
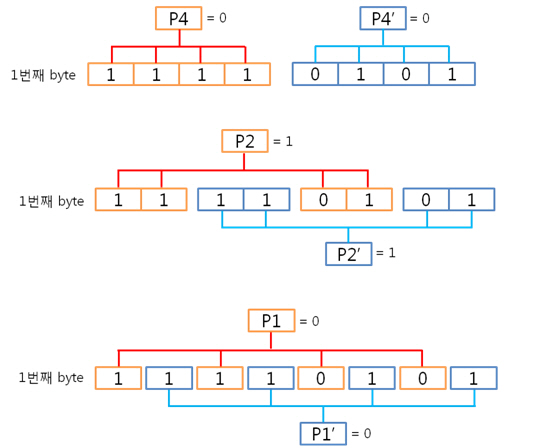
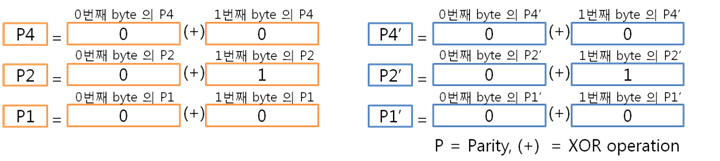
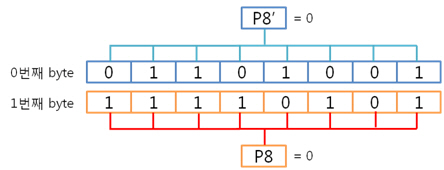
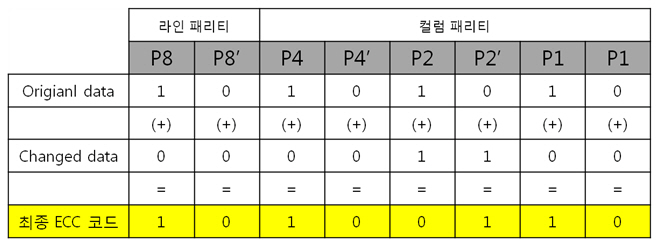
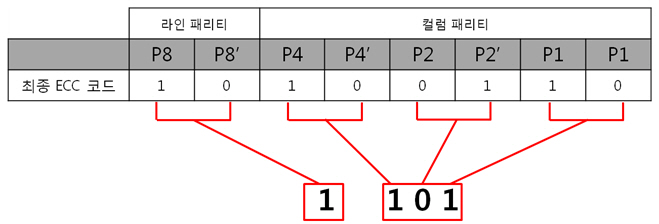
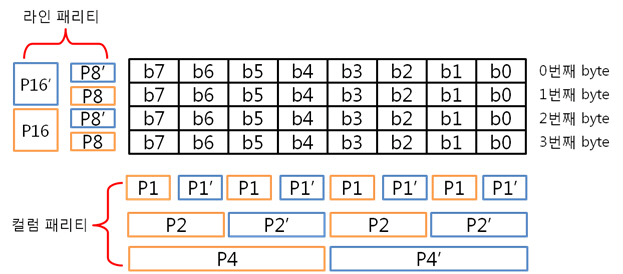
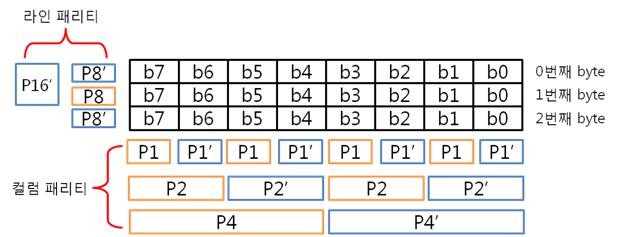
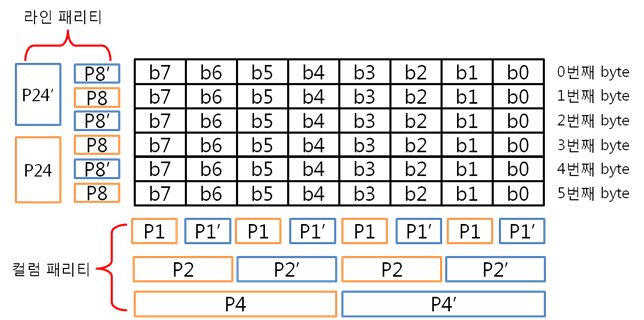
그리고 1번째 byte의 컬럼 패리티를 구합니다. 각 byte의 컬럼 패리티를 구했으니 각 컬럼 패리티를 XOR 연산을 합니다. 이리하여, 2byte의 컬럼 패리티를 구했습니다. 아까도 말했지만 컬럼 패리티는 에러난 열의 위치, 즉 X의 위치를 나타낸다 하였습니다용. 그렇다면 행의 위치, 그러니까 Y의 위치를 나타내는 놈은 없을까요? 네 있습니다. 있고 말고요! 바로 ‘라인 패리티’ 입니다. 2byte의 라인 패리티는 아래의 방법대로 구합니다. 즉 P8, P8’ 패리티 쌍은 연속된 8비트로 계산하는 것입니다. 그래서 라인 패리티를 구하면 드디어 라인 패리티를 구하여 원본 데이터의 ECC 코드가 나왔습니다. 자 원본 데이터와 원본 데이터의 ECC 코드를 NAND에 씁니다. 그런데 또 또 또 어떠한 외부 요인에 의해 데이터가 바뀌었습니다. 그리고 저희는 NAND에 있는 바뀐 데이터를 읽습니다. 위에 보면 1byte의 5번째 bit가 에러가 있습니다. 하지만 읽은 데이터가 원본인지 아닌지 모르기 때문에 읽은 데이터의 ECC 코드를 생성합니다. 방법은 같습니다. 컬럼 패리티를 구하고, 라인 패리티를 구하면 됩니다. 0번째 byte의 컬럼 패리티를 구합니다. 1번째 byte의 컬럼 패리티를 구합니다. 2byte의 컬럼 패리티를 구합니다. 컬럼 패리티를 구했으니 라인 패리티를 구합시다. 라인 패리티까지 구하여 읽은 데이터의 ECC 코드를 만들었습니다. 그럼 원본 데이터의 ECC 코드와 비교를 해보죠! 드디어 2byte의 최종 ECC 코드를 구했습니다. 이 최종 ECC 코드의 패리티 쌍을 표현식으로 바꾸어 에러가 난 비트를 찾아 보죠! 짜잔! 라인 패리티는 ‘1’을, 컬럼 패리티는 ‘101’ 이라는 결과가 나왔습니다. 이것을10진수로 바꾸어 보면 라인 패리티는 1, 컬럼 패리티는 5 라는 숫자가 나옵니다. 우와! 에러가 난 위치는 1번째 byte(행)의 5번째 bit(열) 이군요!. 라인 패리티는 Y의 위치를, 컬럼 패리티는 X의 위치를 찾는 것이라 생각하시면 되겠습니다. 4. 4byte의 ECC 코드를 만들자. 2byte 에서 1bit 에러는 위와 같이 찾았는데 그렇다면! 4byte 에서 1bit 에러는 어떻게 찾을까요? 그런데 어라?? 왜 3byte 에서 1bit 에러는 검사 안하나요? 라는 의문을 가진 당신. 질문을 해주셔서 감사합니다. 뭐 3byte 에서 1bit 에러는 검사를 못합니다. 아니 왜~!? 못하는 것일까요? 먼저 아래의 4byte 일때 라인 패리티 쌍을 보시면 연속된 16bit를 이용해 P16, P16’ 라는 패리티 쌍이 나오네요. 쌍입니다. 쌍(욕 아니에요). 그렇다면 3byte 일때는? 오호통제라~. 라인 패리티인 P8’과 P16’의 쌍이 없습니다. 이러면 곤란하죠! 그렇다면 쌍만 존재하면 다 되는 것인가? 라는 의문이 듭니다. 결론은 안됩니다. 위에 보시면 P24, P24’라는 쌍이 존재하지만 제가 직접 해본 결과 컬럼 패리티를 이용해 X의 위치는 알 수 있지만, 라인 패리티를 이용해 Y의 위치는 확인이 안됩니다. 결국, 행의 증가는 2의 승수만큼 증가해야 한다는 말입니다. 즉, 1, 2, 4, 8, 16, 32, 64, 128, 256 … byte로 되야 한다는 말입니다. 자 그럼 바로 4byte 건너 띄고 한번 8byte 에서 1bit 에러 찾는 것을 해보겠습니다. 다음 시간에요. http://ms-osek.org/ 에 오시면 좀 더 빠르게 보실 수 있습니다. 많이 놀려 와주세요! 참고자료) 삼성 NAND Flash ECC Algorithm

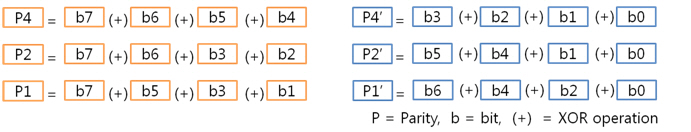





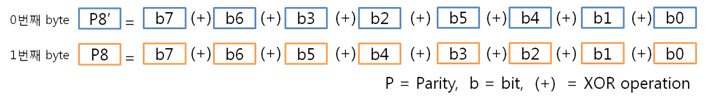

- 1. 원본 byte.jpg (17.0KB)(321)
- 2. 1byte ECC 구하는 방법.jpg (61.9KB)(306)
- 3. 1byte ECC 규칙.jpg (66.5KB)(317)
- 4. 원본 1byte.jpg (17.0KB)(261)
- 5. 1byte ECC 구하기.jpg (83.3KB)(263)
- 6. 1byte ECC.jpg (13.7KB)(242)
- 7. 예로.jpg (64.3KB)(246)
- 8. 변한 1byte 구하기.jpg (75.7KB)(253)
- 9. 변한 1byte ECC.jpg (13.4KB)(221)
- 10. 1byte 최종 ECC.jpg (46.5KB)(227)
- 11. 1byte 표현식.jpg (25.8KB)(220)
- 12. 2byte 원본.jpg (25.2KB)(240)
- 13. 2byte 패리티 구하는 방법.jpg (70.8KB)(267)
- 14. 0번째 byte 구하기.jpg (64.1KB)(220)
- 15. 1번째 byte 구하기.jpg (62.5KB)(251)
- 16. 2byte 패리티 구하기.jpg (73.6KB)(299)
- 17. 2byte 패리티 구함.jpg (17.5KB)(193)
- 18. 2byte 라인 패리티 규칙.jpg (48.5KB)(250)
- 19. 2byte 라인 패리티 계산.jpg (39.1KB)(216)
- 20. 2byte 라인 패리티 진짜 계산.jpg (40.6KB)(247)
- 21. 2byte ECC 코드.jpg (25.4KB)(248)
- 22. 바뀐 2byte.jpg (25.9KB)(258)
- 23. 바뀐 2byte 0번째.jpg (69.3KB)(206)
- 24. 바뀐 2byte 1번째 컬럼 패리티.jpg (71.7KB)(265)
- 25. 바뀐 2byte 컬럼 패리티.jpg (69.5KB)(212)
- 26. 바뀐 2byte 컬럼 패리티 표.jpg (17.7KB)(308)
- 27. 바뀐 2byte 라인 패리티 구하기.jpg (36.6KB)(220)
- 28. 바뀐 2byte ECC 표.jpg (25.5KB)(231)
- 29. 원본과 비교.jpg (60.4KB)(266)
- 30. 2byte 최종 ECC 표현식.jpg (49.6KB)(389)
- 31. 4byte 패리티 쌍.jpg (87.8KB)(292)
- 32. 3byte 패리티 쌍.jpg (73.5KB)(232)
- 33. 6byte 패리티 쌍.jpg (106.4KB)(280)



와우 이거 정말 대단하군요.. 이걸 이해하고 코딩하려면 OTZ
삼성에서는 이걸 C 코드로 구현해서 제공했으면 합니다. ㅠㅠ
참고로 S3C6410 HWECC-1 bit 계산과 S5PV210 HWECC-1 bit 계산값은 같지 않습니다.,