
강좌 & 팁
안녕하십니까.
삼성의 1bit용 NAND Flash ECC 알고리즘을 해부해 볼 호서대학교에 재학 중인
MS-OSEK Team의 지정웅 입니다.
오늘로써 NAND ECC 알고리즘의 마지막 편이 다가왔습니다. 정말 짧고 굵게 하는 것 같습니다. 제 키처럼요 ㅋㅋㅋ ㅠㅠㅠㅠㅠㅠ
어쨌든 오늘은 256, 512 byte에서 삼성 NAND Flash ECC 알고리즘을 이용하여 ECC 코드 생성, 에러의 판별 기준,
에러의 검출방법, 에러의 종류 등에 대해 알아보도록 하겠습니다.
먼저 지난 시간의 내용을 복습하도록 하죠!.
1. Previously on NAND ECC
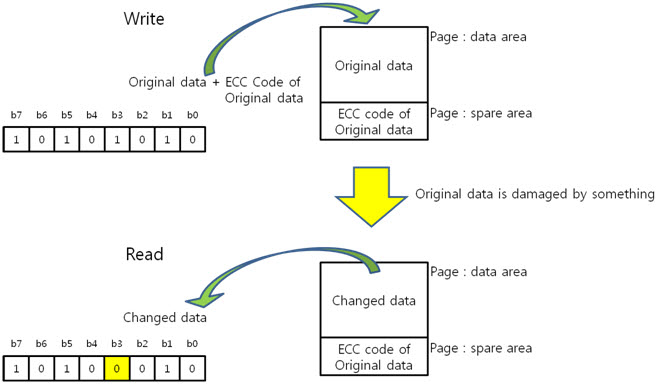
NAND는 가격대비 성능이 좋지만 데이터 연산 중 파워가 나가거나 여러 상황에 의해 데이터가 깨질 수 있습니다. 그렇기에 원본 데이터에 대한 ECC 코드를 만들어 spare영역에 저장하고 변환된 데이터의 ECC 코드를 만들어 비교를 하여 에러를 찾아 NAND의 안정성을 높입니다.
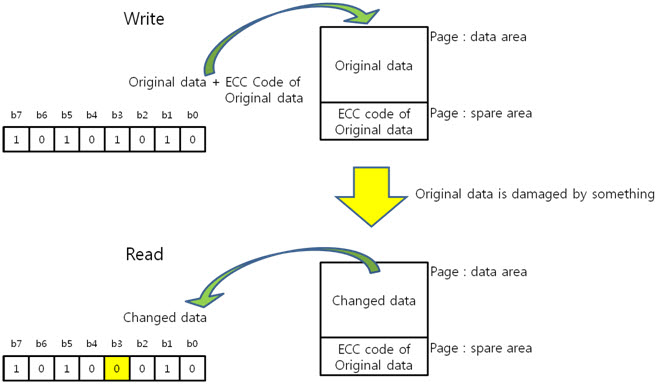
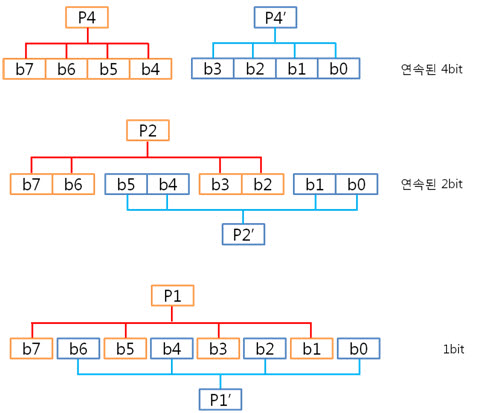
ECC 코드는 ‘컬럼 패리티’와 ‘라인 패리티’로 이루어져 있습니다. 컬럼 패리티는 X의 위치를, 라인 패리티는 Y의 위치를 찾는데 쓰입니다.
아래는 4byte 일때 라인 패리티 쌍과 컬럼 패리티 쌍과
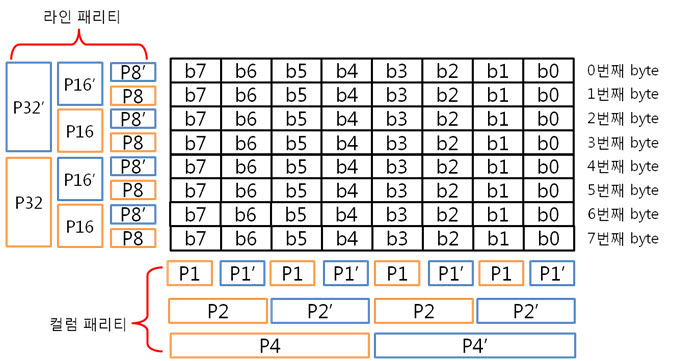
8byte 일때 라인 패리티 쌍과 컬럼 패리티 쌍을 나타낸 것입니다.
4byte)
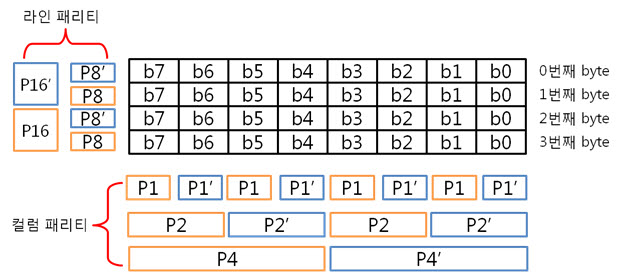
8byte)
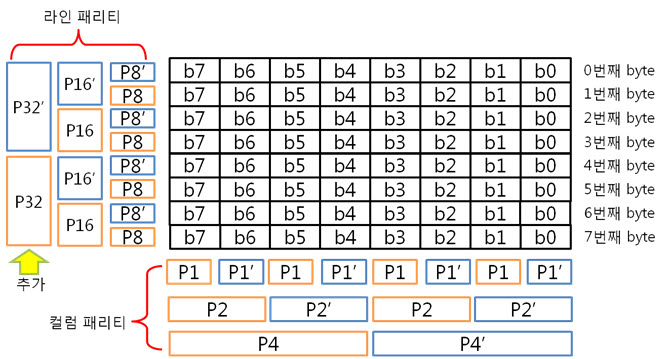
비교해보니 컬럼 패리티 쌍은 추가되지 않았지만 P32, P32’라는 라인 패리티 쌍은 추가 되었습니다.
행이 증가하여도 컬럼 패리티는 증가하지 않고 라인 패리티만 증가하는군요.
맞습니다. X의 크기는 1byte(8bit)로 고정이지만 Y의 크기는 변하게 됩니다. 그러므로, Y의 크기가 16, 32, 64, …, 256, 512byte로 증가할 지라도 1bit 에러를 찾을 때에는 라인 패리티 쌍만 증가한다는 것입니다!. 아 ECC 뭐 별거 없구만유.
ECC 코드를 이용해 에러의 위치를 찾는다고 하였지만 원본 데이터나 변환된 데이터 ECC 코드로는 X, Y의 위치를 찾지 못합니다.
아래와 같이 최종 ECC 코드를 만들어 에러난 X, Y의 위치를 찾습니다.
원본 데이터의 ECC 코드 (+) 변환된 데이터의 ECC 코드 = 최종 ECC 코드
이렇게 나온 최종 ECC 코드를 표현식으로 바꾸어 에러가 난 비트의 X, Y의 위치를 찾습니다. 표현식을 만드는 규칙은 아래와 같습니다.
ex) 패리티의 쌍을 이용해 표현식으로 바꾼다. (P4와 P4’쌍, P2와 P2’쌍, P1과 P1’쌍)
예를 들어 P4 = 0, P4’ = 0 일 경우, 표현은 0
P4 = 1, P4’ = 0 일 경우, 표현은 1
P4 = 0, P4’ = 1 일 경우, 표현은 0
P4 = 1, P4’ = 1 일 경우, 표현은 1
아래 예를 보면 번뜩! 하고 떠오르실 겁니다.
ex) 8byte의 원본 데이터 ECC 코드와 바뀐 데이터 ECC 코드를 이용해 최종 ECC
코드를 만들고 이를 표현식으로
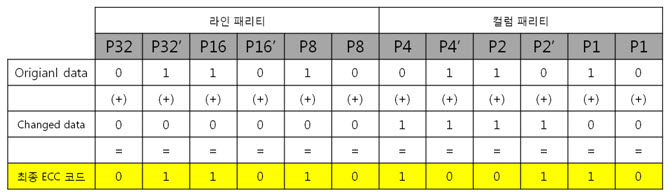
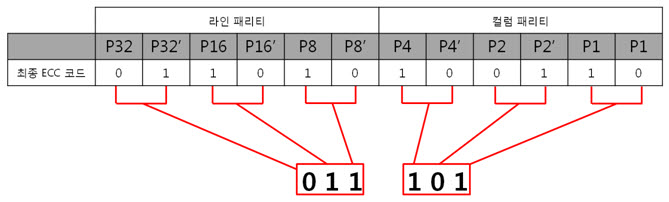
라인 패리티 ‘011’을, 컬럼 패리티 ‘101’ 이라는 결과를 10진수로 바꾸어 보면 라인 패리티는 3, 컬럼 패리티는 5 라는 숫자가 나옵니다. 에러가 난 위치는 3번째 byte(행)의 5번째 bit(열) 입니다.
라인 패리티를 이용해 Y의 위치를, 컬럼 패리티를 이용해 X의 위치를 찾는 것 이라 생각하면 됩니다.
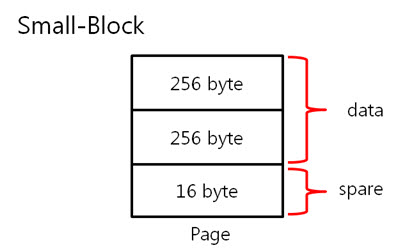
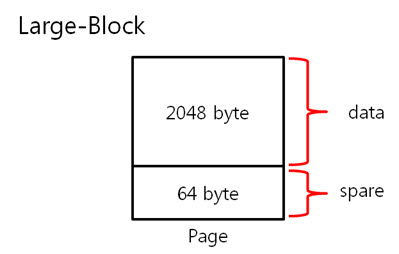
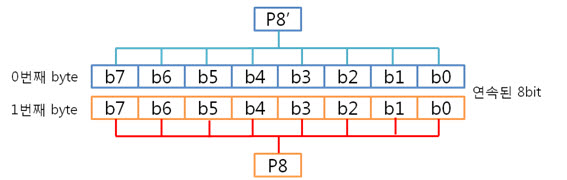
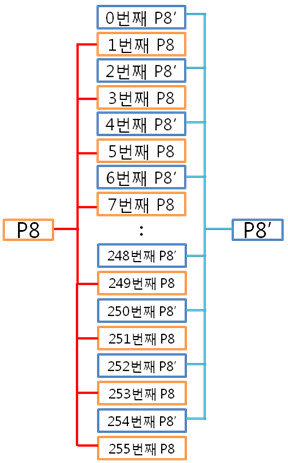
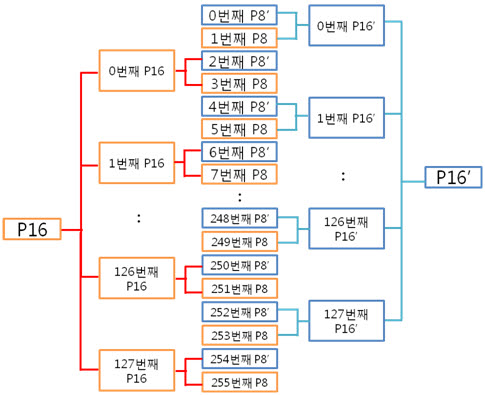
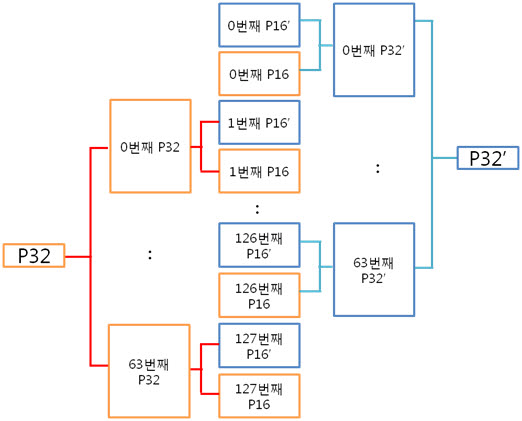
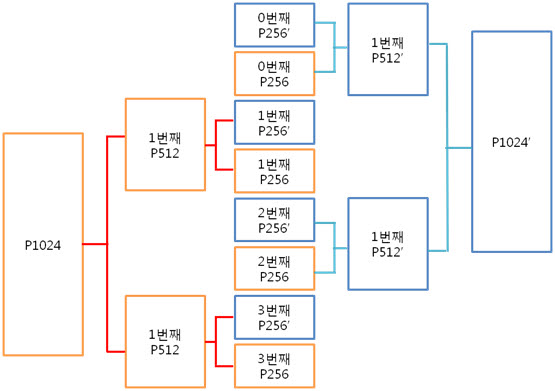
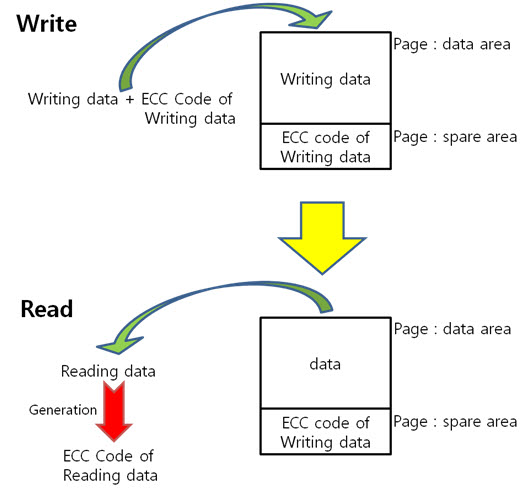
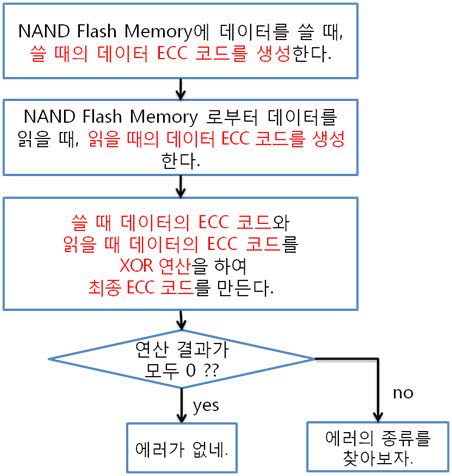
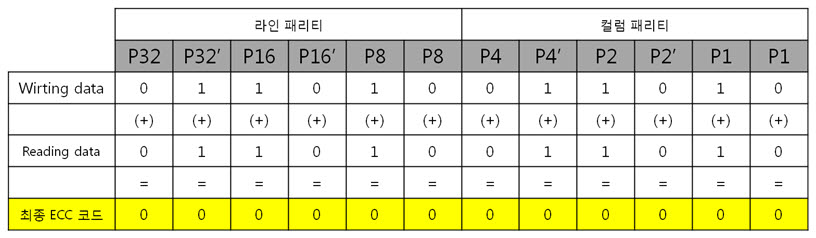
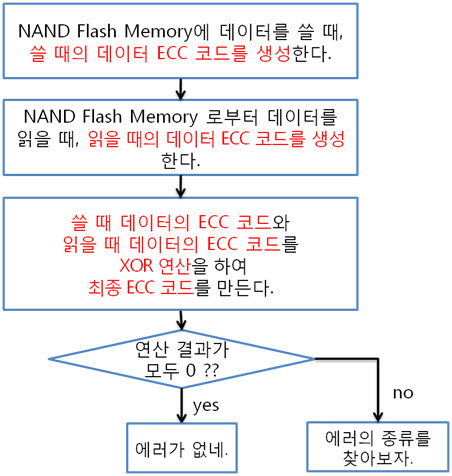
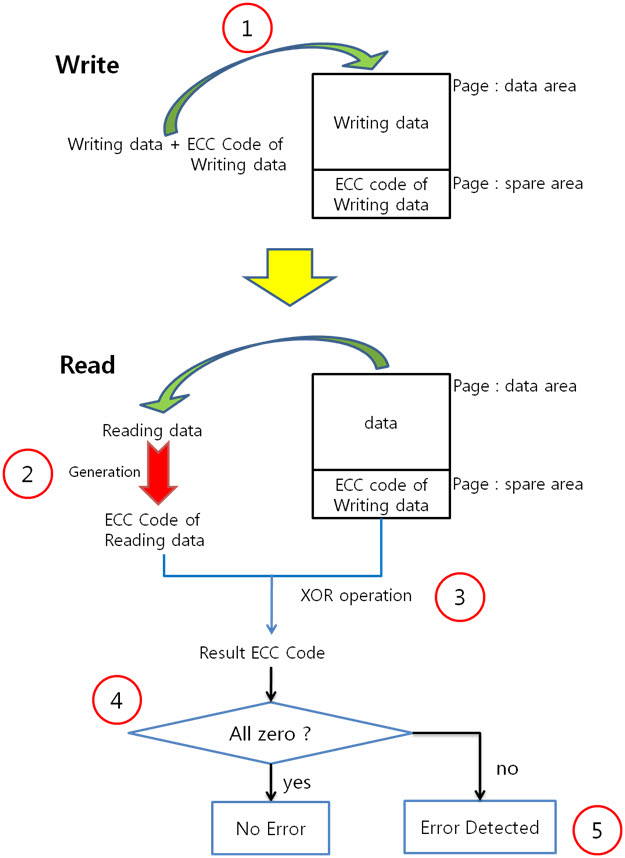
2. 256byte 의 ECC 코드 NAND는 크게 Small-Block과 Lagrg-Block으로 나눌 수 있습니다. Small-Block의 Page는 512byte의 data 영역 + 16byte의 spare 영역으로 이루어져 있습니다. 그리고 Page의 data 영역은 256 + 256 byte로 2개의 공간으로 나누어져 있습니다. Large-Block의 Page는 2048byte의 data 영역 + 64byte의 spare 영역으로 이루어져 있습니다. Large-Block의 Page의 data 영역은 그냥 2048 byte로 1개의 공간입니다. 그런데 뜸금없이 이 말을 왜 할까요???. 네 ~, Small-Block의 경우 Page의 data 영역이 256 + 256 byte 이기 때문에 256byte 혹은 512byte의 ECC 코드를 만들어 NAND의 안정성을 높이는 것입니다. 그럼, Large-Block의 경우 몇 byte ECC 코드를 만들어 NAND의 안정성을 높일까요? 답은 저도 정확히는 모릅니다. 다만, 제 생각에는 이렇습니다. (온니 제 생각!) NAND는 쓰기/지우기 속도는 빠르지만 읽기 속도는 느립니다. 읽기 속도가 느린데다 2048byte 크기를 읽고 이것을 ECC 코드를 만든 다음에 원본 ECC 코드와 비교해야 하는데 딱 봐도 오래 걸릴 것 같은 느낌이 듭니다. 또한, 2048byte의 1byte보단, 4개의 영역으로 나누어 512byte씩 ECC 코드를 저장하면 2048byte의 4bit를 찾을 수 있으니 NAND의 안정성도 높일 수 있지 않을까라는 생각을 해봅니다. 스페어 영역도 64byte나 되니 ECC 코드를 저장할 공간도 많고 뭐... 그냥 저의 생각! 그렇습니다. (내용을 알고 계신 분은 댓글 부탁드립니다. ㅠㅠㅠ) 자 각설하고 아래의 8byte 일때 라인 패리티 쌍과 컬럼 패리티 쌍을 나타낸 것과 256byte일 때 라인 패리티 쌍과 컬럼 패리티 쌍을 나타낸것을 보시죠. 8byte) 256byte) 256byte 경우에도 X축은 1byte(8bit)로 고정이기 때문에 컬럼 패리티 비트는 증가하지 않습니다. 하지만 Y축은 행이 증가하기에 라인 패리티 비트가 증가하는 것을 보실 수 있습니다. 그럼 ECC 코드를 구성하는 컬럼 패리티와 라인 패리티 구해야 하는데, 256byte의 컬럼 패리티는 어떻게 구할까요? 역시나, 저번시간에 봤던 1byte 컬럼 패리티 구하는 방법을 보도록 하죠. 기네~ 컬럼 패리티는 이렇게 구하는 것이였어. 그럼 256byte의 컬럼 패리티는 어떻게 구해야 할까요? X의 위치를 나타내는 컬럼 패리티를 아래와 같은 방법으로 구합니다. 위와 같이 연산하여 컬럼 패리티를 구하였으면, 이제는 라인 패리티를 구해야겠습니다요. 256byte의 라인 패리티는 아래와 같이 구할 수 있습니다. 먼저 P8, P8’를 구하는 것을 보면 연속된 8bit를 XOR 연산을 하여 P8, P8’를 만드네요. 그렇다면 256byte의 P8, P8’는 아래와 같겠군요. 그리고 P16, P16’는 P8, P8’를 이용하여 구합니다. 마찬가지로 P32, P32’는 P16, P16’로, P64, P64’는 P32, P32’로 구하는 것이지요. 이렇게 이전 라인 패리티 쌍을 이용하여 다음 라인 패리티 쌍을 구하는 것입니다. : : 위와 같은 과정을 거쳐 라인 패리티를 구할 수 있습니다. 이로써 데이터의 ECC 코드를 구하는 것입니다. 3. 에러 검출 순서, 에러 판별 기준. 먼저 아래를 보도록 하죠. ① 원본 데이터와 바뀐 데이터만 존재하는 경우 ② 일반적으로 NAND에 데이터를 쓰고, 읽는 경우 이제부터는 ② 의 기준으로 설명을 하면 최종 ECC 코드는 아래와 같이 만들 수 있습니다. 쓸 때 데이터의 ECC 코드와 읽을 때 데이터의 ECC 코드를 가지고 아래와 같이 최종 ECC 코드를 만듭니다. 쓸 때 데이터의 ECC 코드 (+) 읽을 때 데이터의 ECC 코드 = 최종 ECC 코드 자, 에러를 검출하는 순서도를 보시죠. 순서도를 보시게 되면 에러를 판단하는 기준은 연산 결과가 모두 0 이다, 아니다 라는 것입니다. 연산 결과가 모두 0 이라는 소리는 원본 데이터의 ECC 코드와 바뀐 데이터의 ECC 코드의 내용이 같다는 소리입니다. ex) 8byte에서 쓸 때 데이터의 ECC 코드와 읽을 때 데이터의 ECC 코드가 같은 경우 최종 ECC 코드를 보시면 모든 비트가 ‘0’ 입니다. 이럴 때에는 에러가 없다!. 라는 것입니다. 4. 에러의 종류. 다시 에러 검출 순서도를 보시면, 연산 결과, 최종 ECC 코드의 모든 비트가 ‘0’이 아니면 에러의 종류를 찾아야 합니다. 에러의 종류는 다음과 같습니다. ① 수정 가능한 에러 ② ECC 에러 ③ 수정 불가능한 에러 ① 수정 가능한 에러 최종 ECC 코드에서 ‘1’인 비트의 합계 == ECC 코드 / 2 일 경우 수정 가능한 에러 입니다. 아래의 예를 보시면서~ 이해팍, 이해팍팍, 이해팍 이해팍팍! 2byte 일때) ECC 코드의 총 개수는 8개, ‘1’의 합계는 4, ECC 코드(8) / 2 = 4 4byte 일때) ECC 코드의 총 개수는 10개, ‘1’의 합계는 5, ECC 코드(10) / 2 = 5 8byte 일때) ECC 코드의 총 개수는 12개, ‘1’의 합계는 6, ECC 코드(12) / 2 = 6 256byte 일때) ECC 코드의 총 개수는 22개, ‘1’의 합계는 11, ECC 코드(22) / 2 = 11 512byte 일때) ECC 코드의 총 개수는 22개, ‘1’의 합계는 12, ECC 코드(24) / 2 = 12 ② ECC 에러 최종 ECC 코드에서 ‘1’인 비트의 개수가 딱 하나만 있을 때를 말합니다. 이는 ECC 코드(라인, 컬럼 패리티) 자체의 에러입니다. 그렇기 때문에 NAND에 저장한 데이터는 에러가 난게 아니라는 소리입니다. 그래서 ECC 코드만 다시 저장시키면 되겠습니다용!. ③ 수정 불가능한 에러 위의 2가지 경우를 제외한 모든 경우입니다. 이는 에러난 비트의 개수가 2비트 이상이라는 것입니다. 이럴 경우에는 데이터를 고칠 수가 없습니다. 왜냐하면 우리는 1bit 에러를 수정하는 것이기 때문입니다. 5. 깔끔 정리!. 깔끔하게 5줄로 정리를 하겠습니다. 1. 쓸 때 데이터의 ECC 코드를 만들어 Spare 영역에 저장한다. 2. 읽을 때 데이터의 ECC 코드를 만든다. 3. 쓸 때 데이터의 ECC 코드와 읽을 때 데이터의 ECC 코드를 XOR 연산을 한다. 4. 이렇게 만들어진 최종 ECC 코드의 결과로 에러 판별 5. 에러 종류를 파악한다. 어떻게 이해가 팍팍 오시나요? 너무 초간단히 정리해서 모르시겠다고요~!? 그렇다면, 한번씩 더 읽어주세요. 조회수 올라가게 ㅎㅎㅎ 이상입니다. 이로써 삼성 NAND Flash ECC 알고리즘에 대해 3주간 해부를 해보았습니다. 정말 준비하면서 많은 것을 느낄 수 있었습니다. 그동안 읽어 주셔서 감사합니다!.







- 1. 원본, 바뀐 데이타.jpg (35.4KB)(320)
- 2. 4byte 패리티들.jpg (48.2KB)(185)
- 3. 8byte 패리티들.jpg (75.1KB)(208)
- 4. 8byte 최종 ECC 코드.jpg (32.3KB)(214)
- 5. 8byte 표현식.jpg (28.0KB)(208)
- 6. 스몰 블럭 페이지.jpg (12.8KB)(197)
- 7. 라지 블럭 페이지.jpg (11.5KB)(231)
- 8. 8byte 패리티들.jpg (74.0KB)(195)
- 9. 256byte 패리티들.jpg (65.4KB)(290)
- 10. 1byte 컬럼패리티.jpg (37.9KB)(152)
- 11. 256byte 컬럼패리티.jpg (79.2KB)(213)
- 12. 2byte 라인패리티.jpg (25.9KB)(206)
- 13. 256byte P8, P8'.jpg (34.7KB)(176)
- 14. 256byte P16, P16'.jpg (46.9KB)(164)
- 15. 256byte P32, P32'.jpg (37.2KB)(169)
- 16. 256byte P1024, P1024'.jpg (40.4KB)(191)
- 17. 원본, 바뀐 데이타.jpg (35.4KB)(302)
- 18. 쓸때 읽을때 데이타.jpg (36.1KB)(258)
- 19. 에러 검출 순서도.jpg (61.8KB)(1,480)
- 20. 에러없음.jpg (47.6KB)(168)
- 21. 에러 검출 순서도.jpg (61.8KB)(262)
- 22. 2byte 일때.jpg (13.5KB)(164)
- 23. 4byte 일때.jpg (18.7KB)(165)
- 24. 8byte 일때.jpg (20.3KB)(178)
- 25. 256byte 일때.jpg (21.8KB)(166)
- 26. 512byte 일때.jpg (25.0KB)(157)
- 27. 초간단 정리.jpg (70.4KB)(663)


