휴게실
1. 상자가 세 개(A, B, C) 있다. 하나에는 자동차가 나머지 둘에는 염소가 들어있다.
2. 사회자는 어느 상자에 뭐가 들어 있는지 알지만, 참가자는 모른다.
3. 참가자가 어느 상자 하나(A)를 골랐다. 그러자 사회자가 B나 C 중에서 염소가 들어있는 상자 하나를 연다. 그리고 묻는다. "선택을 바꾸겠습니까?"
문제) 참가자는 선택을 바꾸는게 (확률적으로) 유리한가, 바꾸지 않는게 유리한가?
[출처] 몬티홀 문제의 정답 (!!!) / 영화 21|작성자 zzang770704
이게 바로 그 유명한 몬티홀 문제 입니다.
실제로 이런 질문을 받을일이 없다고 가정 했을때는 그냥 귀차니즘으로 " 아 ~ A 한다니까 !! ~ " 하며 별생각 없이
그 선택을 고수 할지도 모릅니다.
실제로 생각해 보면 어차피 셋중 하나 아닌가? ㅎ 하는 생각도 들지요.
한번더 기회를 주지만, 처음에 선택한 A 가 자동차 인지 염소인지 모르기 때문에 사회자가 열어보여준 상자는
관심이 없습니다
하지만 확률적으로 계산해 보면 이야기는 달라집니다.
처음 선택 할때는 분명 세개중에 한개를 선택 하므로 1/3 확률이죠, 여기까지는 누구나 다 압니다
하지만 사회자가 하나의 문을 열어 보였을때의 확률은 ??....
이제 남은 두 개의 문이 있고, 선택권이 있으니, 확률은 1/2 이 아닌가 ??
실제 몬티홀 문제는 위에서 질문한 유리한가 아닌가의 문제가 아니라 확률이 1/2 이냐 2/3 냐 하는
문제 였습니다.
몬티 홀 문제를 정확히 설명하는 조건부확률
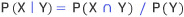(수식 출처 네이버 )
위 수식을 풀어보면 안다고 하지만 .... ㅋ 귀찮고 ;;
어차피 참가자가 처음 선택 할 수 있는 상황을 볼때 세가지 상황이 나오므로,
선택을 바꿨을때의 상황을 전부 나열해 봅시다.
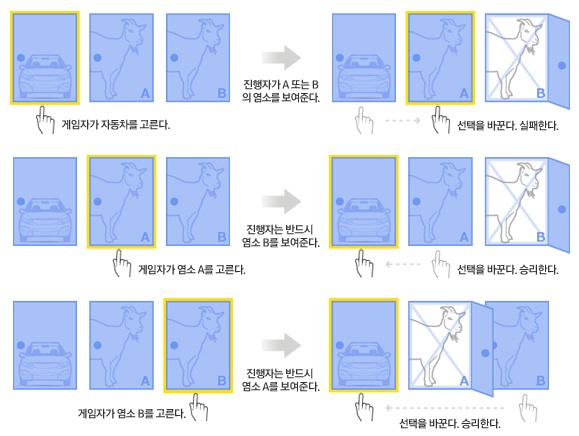
(이미지 출처 NAVER 검색 )
2/3 가 맞군요 ㅎㅎ
이 몬티홀 문제는 영화에서도 재미있게 나왔군요 .
33.3%를 얹어 주셔서 감다 하다는군요 ㅋㅋㅋ
